本文共 4415 字,大约阅读时间需要 14 分钟。
A. Strange Functions(水题)


题意:求 中有多少不同的
值,
发现 g(x) 的值表示的是 10的 该数后缀0个数 次幂,只有后缀0个数改变时g(x)的值才会变化,所以直接输出n的位数
(看题干嘛 看样例
#includeusing namespace std;typedef long long ll;typedef unsigned long long ull;const double eps = 1e-8;const double PI = acos(-1.0);const int N = 35;const int mod = 998244353;const int inf = 0x3f3f3f3f;int main() { int t; string s; scanf("%d", &t); while(t--) { cin >> s; cout << s.size() << '\n'; } return 0;}
B. Jumps (思维)


题意:要从x轴的0位置移动到x位置,第 i 次移动可以选择向左移动一个单位或者向右移动 i 个单位,问最少需要几次移动。
思路:发现先向右走 i - 1 步和向右走 i 步之间的步数可以由把 i 步中的某一步换成 -1 来凑成,i 步的总位移为1 + 2 + 3 + ... + i,把某一步换掉即从总步数的基础上 -2、-3、... - i - 1,但是 -1不可以,所以-1直接向左走一步。
#includeusing namespace std;typedef long long ll;typedef unsigned long long ull;const double eps = 1e-8;const double PI = acos(-1.0);const int N = 1415;const int mod = 998244353;const int inf = 0x3f3f3f3f;int main() { int t, n; scanf("%d", &t); while(t--) { scanf("%d", &n); int stp = 0; while(n > 0) n -= ++stp; if(n == -1) stp++; printf("%d\n", stp); } return 0;}
C. Ping-pong(思维)


题意:两个人打兵乓球,接球和发球都会消耗一点体力,在接球时可以选择接或不接,每一轮最后没有接球的那个人输,上一轮获胜的人在下一轮发球,直到两人体力都变为0时游戏结束。现给出两个人的体力值,他们首先最大化自己的获胜次数,其次最小化对方的获胜次数,问最终他们的获胜次数。
思路:alice先发球,并且总是处在被动地位,bob要最大化自己的获胜次数,最优策略就是让自己的所有体力都做出贡献,他可以一直不回球,直至把alice的体力耗完,让alice无法回球,剩下的回合都是bob胜,即bob获胜y次,alice获胜 x - 1 次(最后一点体力发的球被bob接了,无法回球)
#includeusing namespace std;typedef long long ll;typedef unsigned long long ull;const double eps = 1e-8;const double PI = acos(-1.0);const int N = 1415;const int mod = 998244353;const int inf = 0x3f3f3f3f;int main() { int t, x, y; scanf("%d", &t); while(t--) { scanf("%d%d", &x, &y); printf("%d %d\n", x - 1, y); } return 0;}
D. Sequence and Swaps


题意:给一个x和一个序列,每次操作可以把序列种一个大于x的数和x交换,问至少多少次把序列变为非递减的,或者输出不能实现。
思路:序列中共有 cnt 对 a[i - 1] > a[i],从左向右扫一遍,如果当前 cnt > 0 且 a[i] > x,就要进行交换。具体看代码。
#includeusing namespace std;typedef long long ll;const int N = 510;const int inf = 0x3f3f3f3f;const int mod = 1e9 + 7;int a[N];int main() { int t, n, x; scanf("%d", &t); while(t--) { int cnt = 0; scanf("%d%d", &n, &x); for(int i = 1; i <= n; ++i) { scanf("%d", &a[i]); if(i > 1 && a[i - 1] > a[i]) cnt++; } if(!cnt) { printf("0\n"); continue; } int ans = 0; for(int i = 1; i <= n; ++i) { if(cnt > 0 && a[i] > x) { if(i > 0 && a[i - 1] > a[i]) cnt--; if(i < n && a[i] > a[i + 1]) cnt--; swap(a[i], x); if(i > 0 && a[i - 1] > a[i]) cnt++; if(i < n && a[i] > a[i + 1]) cnt++; ans++; } } printf("%d\n", !cnt ? ans : -1); } return 0;}
E. Four Points(思维 + 枚举)





题意:给四个点,通过移动使这四个点构成一个和坐标轴平行的正方形,问最小的移动步数。
思路:
设p1、p2、p3、p4分别为最终要作为正方形左下角、右下角、右上角、左上角的点,首先枚举4个点的排列,共 4! 种。
再枚举边长,为使步数最小,正方形的边长一定是某两点横坐标之差或纵坐标之差,共12种。
现在确定了每个点的相对位置和正方形的边长,求构成这种正方形的最小步数,等价于固定一个点不动,让其他三个点和该点重合的步数,如图:
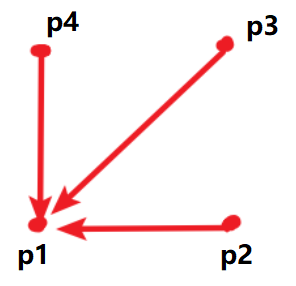
可以先把它们的目标相对距离减掉,也就是p2.x -= d,p3.x -= d,p3.y -= d,p4.y -= d,再把得到的四个新坐标移动到一点,把横纵坐标分开考虑,也就是把4个数变成相同的,取中位数即可。
#includeusing namespace std;typedef long long ll;const int N = 1e5 + 10;const ll inf = 0x3f3f3f3f3f3f3f3f;const int mod = 1e9 + 7;ll x[5], y[5], dis[20], xx[5], yy[5];int main() { int t, p[5]; for(int i = 1; i <= 4; ++i) p[i] = i; scanf("%d", &t); while(t--) { int tot = 0; for(int i = 1; i <= 4; ++i) { scanf("%lld%lld", &x[i], &y[i]); for(int j = 1; j < i; ++j) { dis[++tot] = abs(x[i] - x[j]); dis[++tot] = abs(y[i] - y[j]); } } ll ans = inf; do { for(int i = 1; i <= tot; ++i) { for(int j = 1; j <= 4; ++j) { xx[j] = x[p[j]]; yy[j] = y[p[j]]; } ll d = dis[i]; xx[2] -= d, xx[3] -= d; yy[3] -= d, yy[4] -= d; sort(xx + 1, xx + 5); sort(yy + 1, yy + 5); ll cnt = 0; for(int i = 1; i <= 4; ++i) { cnt += abs(xx[i] - xx[2]); cnt += abs(yy[i] - yy[2]); } ans = min(ans, cnt); } } while(next_permutation(p + 1, p + 5)); printf("%lld\n", ans); } return 0;}
转载地址:http://bcio.baihongyu.com/